OriginStamp: Verifying Proofs
- 4 minutes read - 792 wordsRecently, I wrote about some initial adventures with OriginStamp
Using OriginStamp’s UI or API, submitting a hash results in transactions being submitted to Bitcoin, Ethereum and a German newspaper.
Using the API, it’s possible to query OriginStamp’s service for a proof. This post explains how to verify such a proof.
The diligent reader among you (Hey Mom!) will recall that I submitted a hash for the message:
Frederik Jack is a bubbly Border Collie
The SHA-256 hash of this message is:
037e945cf8da5945acbcf2390c71a497c6edefdc364ada1f33d76a2b5f8b472b
NB Don’t take my word for it, you can test this innumerable ways including, in bash:
printf "Frederik Jack is a bubbly Border Collie" | sha256sum
You may follow along by checking this hash using OriginStamp’s verification tool, choose “hash” and plug in the above value:
https://verify.originstamp.com/
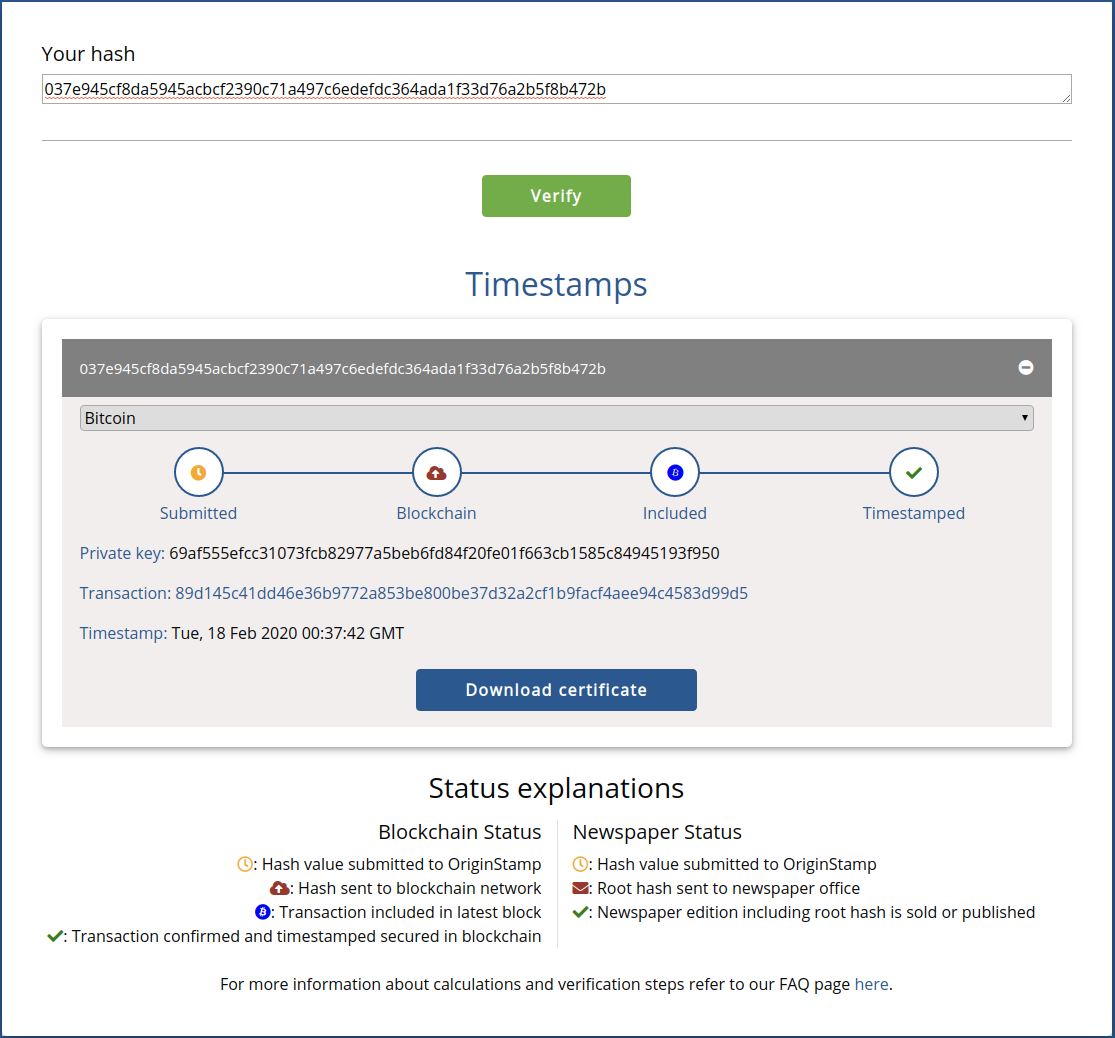
The Bitcoin ID that’s shown is clickable
NB OriginStamp’s German-team uses the German-language version of the site (/de/) which I’ve omitted from this link.
If you have access to OriginStamp’s API, you can request a proof for my hash (currency=0 for Bitcoin; proof_type=1 for PDF) but, without sharing OriginStamp’s document, let’s work through what it provides.
Validate the Proof
It starts with a copy of the Merkle Tree proof:
<?xml version="1.0" encoding="UTF-8"?>
<node value="69af555efcc31073fcb82977a5beb6fd84f20fe01f663cb1585c84945193f950" type="key">
<left value="e4d9506f6a877a6f15c4e240e53327cc7c38ef37e610ebfc62ce674308b3263e" type="mesh">
<left value="ee7536d1855cddf24dba36bfc04cdc1db522cef46e49c4d5aa5bde25648db388" type="mesh">
<left value="9d7c106e64d5e6c40daacb4bcf4397912e31a78fe0e81b9fb4d79da08c7b2808" type="mesh">
<left value="b918032b5cc7185ee2de8d38907e43b9ef9ffb61b5424ebf8a70643721c0af2f" type="mesh">
<left value="4b2b83117d905892053e5f4a4d28316a0107b9a360fce4633361e489b7b1359e" type="mesh">
<left value="10555d6d9b28b8cc551cd2dd99fb270630b2cf2f56f8d70a7893a64b4b57ecb5" type="mesh">
<left value="c54c5350dba05d216175318dbfa6dd732d1adbdc92beaf320443f523f822f01d" type="mesh">
<left value="c7ebc60a38854a4671ea786f14ceff0e7e183f75d6fbda3557292bae3b13f23d" type="mesh"/>
<right value="a97c1a50c069d3397e9702f28ab38a420b537c6e942b8546860f8fb7a49c70e4" type="mesh">
<left value="d1776b7c1b51ad1441bf765e194377ac9060f2402d6e91cee5502d8ca3a99546" type="mesh"/>
<right value="25d8c347fb71a839c1274ec2ebe666b8dd4a3255403d991be39bb10016aa51f1" type="mesh">
<left value="c006e869d7ba65ac4d5105888fee6a6bf6a3b38f23c6300137f003a3988238ae" type="mesh">
<left value="097c397d862795e96abb576eb6bc76365f0235cfa1c938352045d1e62b347b1d" type="mesh"/>
<right value="9407b62021fe6335430fc54090b90e6588ac38421309e279460335b5f94d67fb" type="mesh">
<left value="369cb74a155479eecf22f65337e03a4ad5b935772e2d3348854f3d9d71923960" type="mesh"/>
<right value="e220f15411b706ad10ff9990dc7f760ddfec2ebc61a11204fc5b36e140c17e0b" type="mesh">
<left value="0d899a0e8f72691e3859377c4780a5b54c40e743d1486aeb1e76c038dab9e8ce" type="mesh"/>
<right value="e40a25b8bd05b48675a02c8ad7e0c23b6d62385b0acaffbab63f95e39369ebc7" type="mesh">
<left value="037e945cf8da5945acbcf2390c71a497c6edefdc364ada1f33d76a2b5f8b472b" type="hash"/>
<right value="038df16cfbbeed2f029f00587bfcaa9920d4f7bcaeee60ee788d4a66179709c3" type="mesh"/>
</right>
</right>
</right>
</left>
<right value="c3d44098be84f892ee1fe1c2c6caa52257eb96caaaa3f313edbafdc4a3ba6eae" type="mesh"/>
</right>
</right>
</left>
<right value="5b2e60ccb6907fae79d249bf7943b050c28b5fef84b9b44399f58461dd120c4a" type="mesh"/>
</left>
<right value="c47e581dd90c10aad2cb4121c1a94a3199f9788f4f2e5d0f200f8f167ae2517c" type="mesh"/>
</left>
<right value="dbdfc7af18a876d64d6fa2f0110e5dc6ead648f3e33f9e0163ceb267d47cd90d" type="mesh"/>
</left>
<right value="98f7dafd1f8c6ec84a555819d9cd05baed657e3973f86f3fb178dbd13c676bba" type="mesh"/>
</left>
<right value="36447318383768a406815764e128d404ca1482ec57cd995e12ac97962b33b73e" type="mesh"/>
</left>
<right value="6e7ca4d2ea8919396dfd66a7d57338cb0ce8bca76043b5a4745e463c2c9d9af8" type="mesh"/>
</left>
<right value="0f1301c53b6885f23037a81da41f450968a2b133f28b30d65d1fb431da74a9c1" type="mesh"/>
</node>
I appreciate that presents rather inelegantly but I think it’s best to show the structure.
This is part of a Merkle tree encoded as XML.
The leaf that we’re interested is:
<right value="e40a25b8bd05b48675a02c8ad7e0c23b6d62385b0acaffbab63f95e39369ebc7" type="mesh">
<left value="037e945cf8da5945acbcf2390c71a497c6edefdc364ada1f33d76a2b5f8b472b" type="hash"/>
<right value="038df16cfbbeed2f029f00587bfcaa9920d4f7bcaeee60ee788d4a66179709c3" type="mesh"/>
NB The has value (037e...) is in there.
To verify this tree, we must take the left value (L), the right value (R), concatenate them (LR) and hash the result
L="037e945cf8da5945acbcf2390c71a497c6edefdc364ada1f33d76a2b5f8b472b"
R="038df16cfbbeed2f029f00587bfcaa9920d4f7bcaeee60ee788d4a66179709c3"
printf "${L}${R}" | sha256sum | head --bytes=64
yields: e40a25b8bd05b48675a02c8ad7e0c23b6d62385b0acaffbab63f95e39369ebc7 which, you’ll note, is the XML snippet’s root right node.
We recursively apply this rule, collapsing the tree, until we reach the root node (node), I’ve done it and I can assure you that, the result is:
69af555efcc31073fcb82977a5beb6fd84f20fe01f663cb1585c84945193f950
This proves that this merkle tree is consistent, it’s root value hash matches the hashes of its children.
The tree’s root hash is also the private key that OriginStamp included in the bitcoin transaction mentioned above.
So, now we need to go from this private key to a Bitcoin address.
Determine the Bitcoin Address
This is a rather curious set of steps but it is the process that’s defined by the Bitcoin ‘protocol’ and may be validated using various example, including a serivce that OriginStamp refers to TP’s Bitcoin Address Tests
If you plug the private key (69af555efcc31073fcb82977a5beb6fd84f20fe01f663cb1585c84945193f950) into TP’s site, you’ll see all the intermediate steps to the address: 1DacsJLsyr77YYkWpNGg1H5Mq3mUf84VzB
Now, if we return to the Bitcoin Transaction that was provided by OriginStamp:
89d145c41dd46e36b9772a853be800be37d32a2cf1b9facf4aee94c4583d99d5
You’ll notice that this address (1DacsJLsyr77YYkWpNGg1H5Mq3mUf84VzB) as the first address:
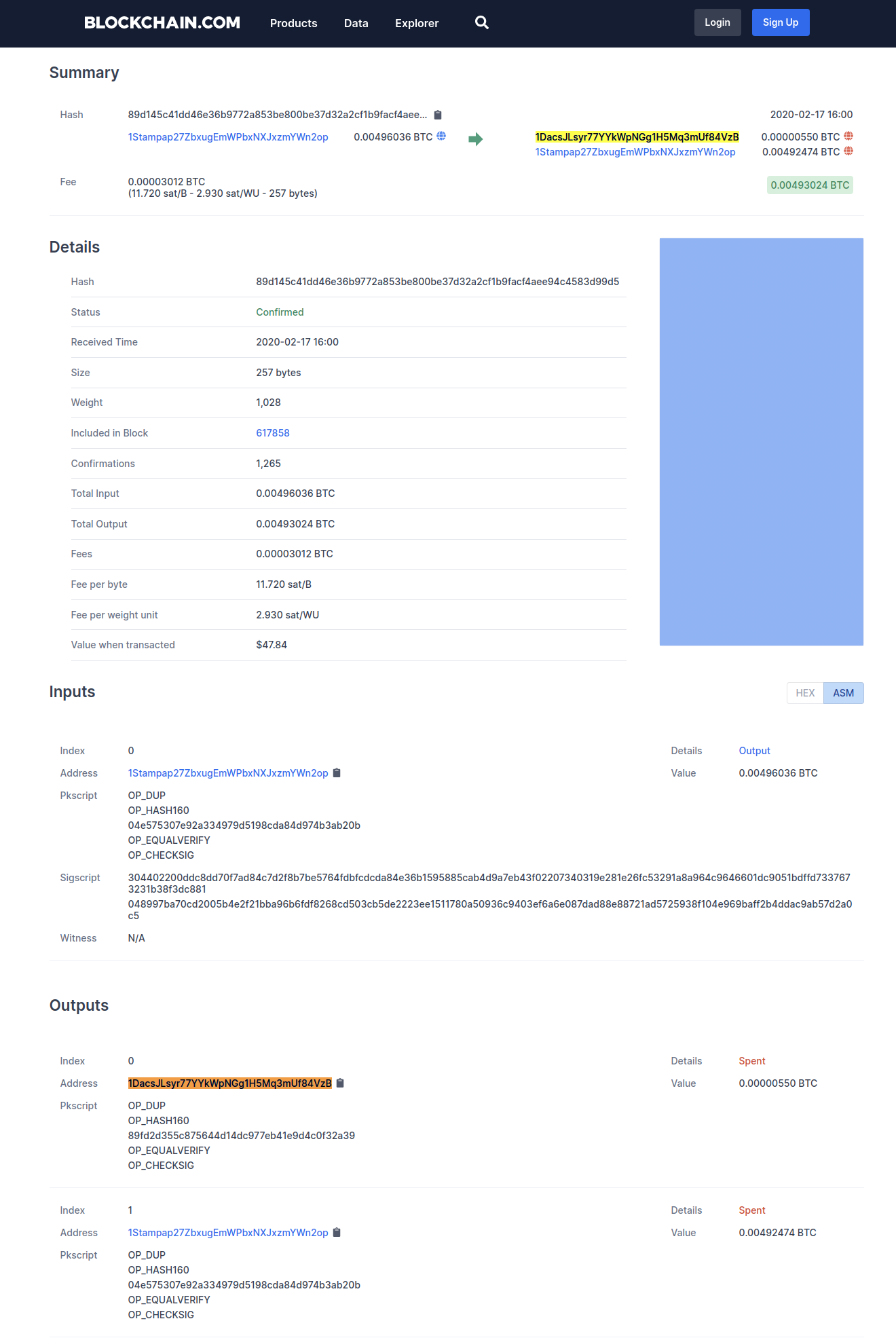
But, how did we get from the private key (69af555efcc31073fcb82977a5beb6fd84f20fe01f663cb1585c84945193f950) to the Bitcoin address?
The site does the work for us, but let’s reproduce it :-)
Step #1: Public Key
This took me the longest time to work out!!
I had help from some friends: https://stackoverflow.com/q/60385053/609290
I had 2 primary issues:
- new(ing) an
ECDSA.PrivateKeyfrom a hex-encoded private key - Identifying that the common default curve (P256 aka secp256r1) was incorrect and that I need to use secp256k1 (and find a Golang implementation)
I learned more about Elliptic Curves too which is always a good thing, including some nitty-gritty on the difference between secp256r1 and secp256k1
Ethereum has a robust Golang implementation and, interestingly (!?) Ethereum and Bitcoin both use secp256k1, so I used Ethereum’s secp256k1 module
Given a secpk256k1 hex-encoded private key , the following Golang function will return the hex-encoded public key:
func Public(privateKey string) (publicKey string) {
var e ecdsa.PrivateKey
e.D, _ = new(big.Int).SetString(privateKey, 16)
e.PublicKey.Curve = secp256k1.S256()
e.PublicKey.X, e.PublicKey.Y = e.PublicKey.Curve.ScalarBaseMult(e.D.Bytes())
return fmt.Sprintf("%x", elliptic.Marshal(secp256k1.S256(), e.X, e.Y))
}
NB I’m unsure whether fmt.Sprintf("%x",....) or hex.EncodeToString(...) is preferable
Step 2: SHA-256 Hash of #1
Not so fast, speedy!
That should read: SHA-256 hash of the (hex) decoded value of #1
// Step #1
s1, _ := hex.DecodeString(publicKey)
// Step #2: SHA-256
h.sha256.New()
h.Write(s1)
s2 := h.Sum(nil)
log.Printf("2: %x", s2)
The good news is that the remaining steps are straightfoward! :-)
The code’s here: https://github.com/DazWilkin/OriginStamp-Proof
HTH!